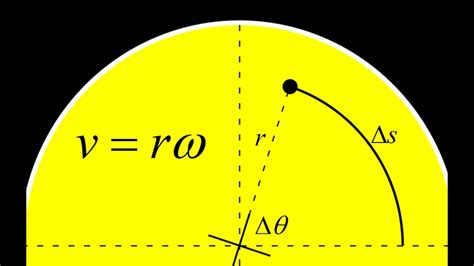
v omega r Consider a point \(P\) moving with constant (linear) velocity \(v\) along the circumference of a circle of radius \(r\). If the angular velocity is \(\omega\), . The Bandana Oversized Scrunchie is the on-trend hair accessory for every day and every activity and brings the perfect touch of paisley print to any outfit.
0 · v r omega derivation
1 · v r omega calculator
2 · v r cross omega or
3 · v and omega relation
4 · relation between v and omega
5 · r omega physics formula
6 · centripetal acceleration formula with omega
7 · angular and linear velocity relationship
FREE Shipping. Allure Homme Sport Eau Extreme Eau De Toilette Spray .
Here is a graphical explanation of $\vec{v} = \vec{r} \times \vec{\omega}$ The vector $\vec{v}$ is perpendicular to the rotation axis .In physics, angular velocity (symbol ω or , the lowercase Greek letter omega), also known as angular frequency vector, is a pseudovector representation of how the angular position or orientation of an object changes with time, i.e. how quickly an object rotates (spins or revolves) around an axis of rotation and how fast the axis itself changes direction.
Angular velocity is represented by the Greek letter omega (ω, sometimes Ω). It is measured in angle per unit time; hence, the SI unit of angular velocity is radians per second. The dimensional formula of angular velocity is [M 0 L 0 T -1]. For .Consider a point \(P\) moving with constant (linear) velocity \(v\) along the circumference of a circle of radius \(r\). If the angular velocity is \(\omega\), . We related the linear and angular velocities of a rotating object in two dimensions in Section 5.1. There, we also already stated the relation between the linear velocity vector .In physics, circular motion is a movement of an object along the circumference of a circle or rotation along a circular arc. It can be uniform, with a constant rate of rotation and constant tangential speed, or non-uniform with a changing rate of .
v r omega derivation
\[\begin{aligned} a_s(t) &= \frac{d}{dt}v_s\[4pt] &=\frac{d}{dt}\omega R=R\frac{d\omega}{dt}\[4pt] a_s(t)&=R\alpha \end{aligned}\] Thus, the linear quantities .Thus, instantaneous velocity has magnitude \(R|\omega|\text{,}\) which is instantaneous speed \(v\text{,}\) and direction in the direction of the tangent to the circle. \begin{equation*} v = R|\omega|, \end{equation*}The formula to calculate the linear speed expressed in meters per second [ m.s^ {-1} m.s−1 ] from the angular velocity expressed in radians per second [ rad.s^ {-1} rad.s−1 ] is: v = r .
The angular velocity - omega of the object is the change of angle with respect to time. The average angular velocity is the angular displacement divided by the time interval: . The velocity is given by this equation $\vec v = \vec \omega \times \vec r$ $\endgroup$ – Farcher. Commented Jun 11, 2018 at 16:45 $\begingroup$ Dear Mr Farcher , In the above equation dtheta/ dt has been rightly defined as angular velocity as i understand and its not angular speed.Please guide $\endgroup$ $\begingroup$ For the above vector (or cross) product, the vector representing the ω is defined as being along the axis of rotation ( the only direction in a rotating system which does not change with time). (Wrap your . In summary, the equation v=r(omega) represents the relationship between velocity and angular velocity, where v is velocity, r is radius, and omega is angular velocity given in radians per second. This can also be understood as the equation for arc length, s=theta*r, where s is arc length and theta is the central angle in radians.
Tour Start here for a quick overview of the site Help Center Detailed answers to any questions you might have Meta Discuss the workings and policies of this site\begin{equation*} v = \omega R = 10,472 \times 0.05 = 524\text{ m/s}. \end{equation*} Checkpoint 5.2.9. Practice with a Friend: Regular and Angular Velocity of Earth. Earth goes around Sun in almost a circular orbit of radius \(1.5\times 10^{11}\text{ m}\) once around in approximately \(365.2425\text{ days}\text{.}\) (a) What is Earth's angular . Here is one simple way. A point is moving around a circle. It has a blue position vector and a red velocity vector, like this: The position vector stays the same length and rotates around and around in a circle.
If you're seeing this message, it means we're having trouble loading external resources on our website. If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked. How do you prove #a=v^2/r# and #a=r\omega^2# using a circle and vector diagram? I know you start off with a circle and two points on the circumference. Each point has an arrow tangent to the circle and are facing the same way (in terms of rotation).
At any instant, the relation v/ r = ω applies to every particle that has a rigid body. If the perpendicular distance of a particle from a fixed axis is r i, the linear velocity at a given instant v is given by the relation, V i = ωr i. Similarly, we can write the expression for the linear velocity for n different particles comprising the system.
Suppose we have a rigid object rotating at some angular velocity $\vec{\omega}$ about some fixed axis. It can be shown that in general, $\vec{v} = \vec{\omega} \times \vec{r}$, where $\vec{r}$ is the instantaneous position of the object. This more general equation does take the directions of the quantities into account via their cross product.. However, it is common .\vec{n}+r The formula for centripetal (radial) acceleration is well known, and there exist many proofs for it: $$||a_c|| = \frac{||v||^2}{r}$$ However, all the proofs I've seen rely on the fact that it is uniform circular motion and the magnitude of .
A sphere rotating around an axis. Points farther from the axis move faster, satisfying ω = v / r.. In physics, angular frequency (symbol ω), also called angular speed and angular rate, is a scalar measure of the angle rate (the . Define angulnr velocity. Derive `v = r omega`Welcome to Doubtnut. Doubtnut is World’s Biggest Platform for Video Solutions of Physics, Chemistry, Math and Bi. Solution. A disk of mass \(M\) and radius \(R\) is placed on an incline at a height \(h\) above the ground. The incline makes an angle \(\theta\) with respect to the horizontal, as shown in Figure \(\PageIndex{3}\). If the disk starts at rest and rolls without slipping down the incline, what speed will the center of mass have when the disk reaches the bottom of the incline?Tour Start here for a quick overview of the site Help Center Detailed answers to any questions you might have Meta Discuss the workings and policies of this site
In physics, angular acceleration (symbol α, alpha) is the time rate of change of angular velocity.Following the two types of angular velocity, spin angular velocity and orbital angular velocity, the respective types of angular acceleration are: spin angular acceleration, involving a rigid body about an axis of rotation intersecting the body's centroid; and orbital angular .Therefore, the angular velocity of the object is thus v/r (in radians per unit of time). The right half portion of the diagram is made by putting the tails of the two v vectors together. Notably, \(\Delta \theta\) is the same in both of the diagrams. . v = \(\omega\) r. Where: \(\omega\) = .The first relationship in v = r ω states that the linear velocity v is proportional to the distance from the center of rotation, thus, it is largest for a point on the rim (largest r), as you might expect.We can also call this linear speed v of a point on the rim the tangential speed.The second relationship in v = r ω can be illustrated by considering the tire of a moving car.
v r omega calculator
v r cross omega or
v and omega relation
nintendo switch messenger bag
Discover ALLURE HOMME SPORT EAU EXTRÊME by CHANEL. A sensual and .
v omega r|v and omega relation